Theory on Union-Find/Disjoint Set Union (DSU)

Disjoint Sets (Union-Find)

Applications

Connected Components in Graph problem
Detecting cycles in graph.
Minimum Spanning Tree (Used in Kruskal's Algorithm)

Theory

Disjoint Set Union is one of easiest data structures to implement.

What are Disjoint Sets:

Sets are called as Disjoint if:

Intersection of any two sets is NULL DSU Data Structure have the same property as stated above and the union of all these disjoint sets is equal to entire set (universal set).

Consider a problem:
You are given several elements each element is a separate set initially. You want to do two kinds of operations:

Combine two given sets
Tell about the connectivity of two elements i.e., whether they are in the same set or not.

Consider the below set, we will be using this input for various approaches:

So as you can see initially all the elements are separate sets.

We will also assign a representative to each set, you can assume that this representative will be the point of contact of this set. Initially each element will be representative of themselves.

For each element you can assume representative as the immediate parent of that element.

Initial State:

Let Combine(u, v) be the operation which combines the set containing the element u and the set containing v.

Lets jump to some combine(u, v) examples to understand better:

Combine(a,b):

So as you can see, elements a & b now belongs to the same set and a is the representative of this set ( representative of both a and b is a).

Combine (c,d):

Combine (e,f):

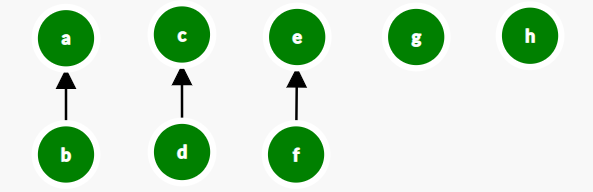
Combine (g,h):

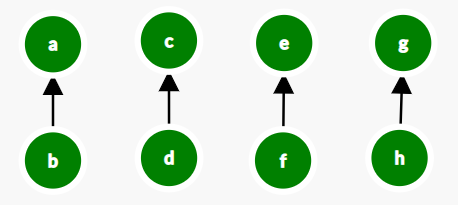
Combine (a,c):

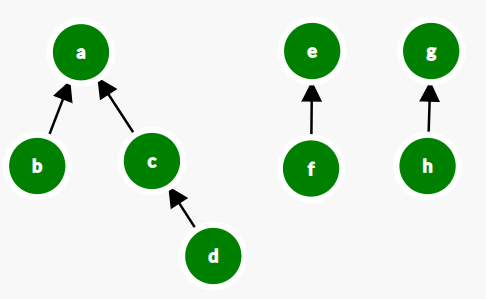
Combine(e,c):

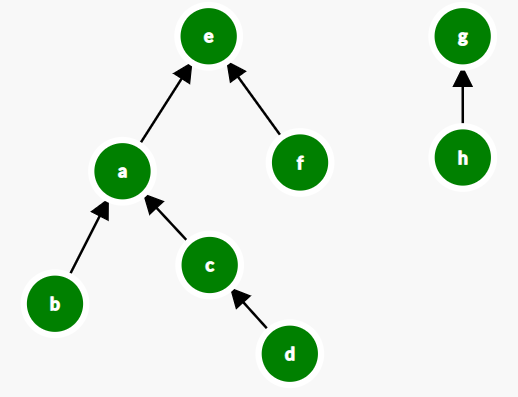
Combine(g,f):

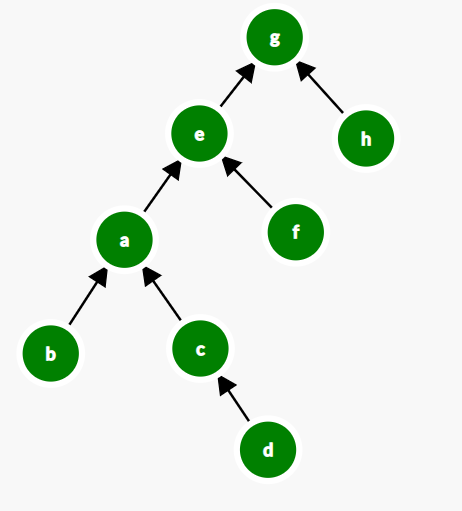
So far we have seen how actually combine function works, lets make it more clear by writing some code:

When we combine two sets, we actually combine the representative of their respective sets. So we need a way to find the representative of an element's set. Lets call that function be find(), which can be defined as:

int find(int u)
{
    if(u == representative[u])
        return u;

    else
        return  find(representative[u]);
}

Lets see if it works or not, currently the representative array looks like below:

Suppose we call find(u) with u = d, then function call will be like below:
representative[d] = c (c!=d) ,
representative[c] = a (a!=c) ,
representative[a] = e (e!=a) ,
representative[e] = g (g!=e) ,
representative[g] = g (g=g hence break)
return g find(d) return g which is actually the representative of the set.

Now we have find() function ready we can combine two sets,

void combine (int u, int v)
{
     u = find(u);
     v = find(v);

     if(u == v)    // already in the same set so no action needed
        return;
    else
       representative[v] = u;
}

We are done with the DSU implementation, its that easy.
To check if two elements are in the same set or not just find their representative using find() and if they are same they belong to the same set.

However our implementation is not much efficient, consider the below case:

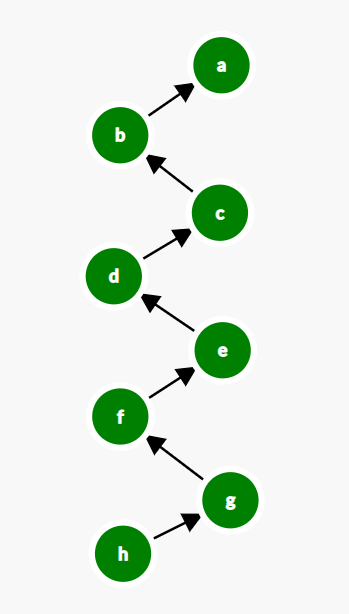
Calling to find() function in cases like above actually will be of O(N).

Union by Size:

We can rectify this problem, we just need to keep the height of the tree as minimum as possible.

Remember when we called combine(u,v) we always make u as the representative of v, however we could have done opposite as well. We can reduce the tree height by comparing the size of sets we are going to combine and always make the bigger set as the representative of the smaller.

Following the above approach the tree after the above combine operations will look like below:

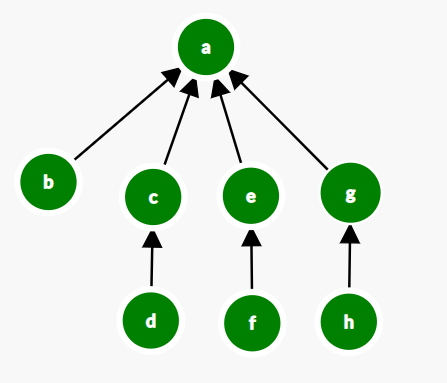
Please verify the above result, you just have to compare the size of sets before combining.

For the set size we have to define an array size[] which will store the size of set.
Initial State:
Updated Combine function:

void combine (int u, int v)
{
    u = find(u);
    v = find(v);

    if(u == v)
        return;

    else
    {
        if(size[u] > size[v])
        {
            representative[v] = u;
            size[u] += size[v];
        }

        else
        {
            representative[u] = v;
            size[v] += size[u];
        }

    }
}

DSU with union by size works in O(log N) which is fast enough to solve alomost all problems, still there is one more optimization possible to the above implementation:

Path Compression:

When we call find() function we traverse the path from given node ‘u’ all upto its representative what if we can set the representative of all the nodes in the path while finding the representative for ‘u’;
See the below updated find() code:

int find(int u)
{
    if(u == representative[u])
        return u;

    else
        return representative[u] = find(representative[u]);
}

Example:
See the graph initially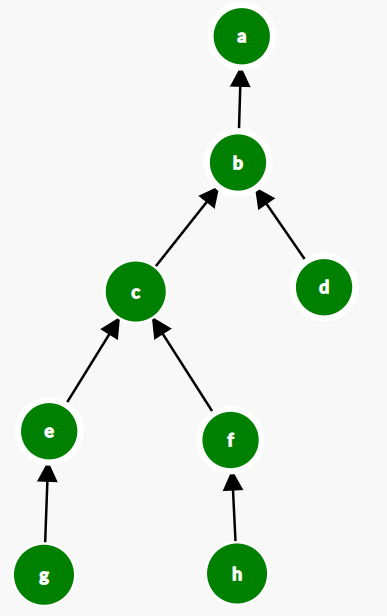

Now if a call is made to find(g), then the graph will be transformed to :

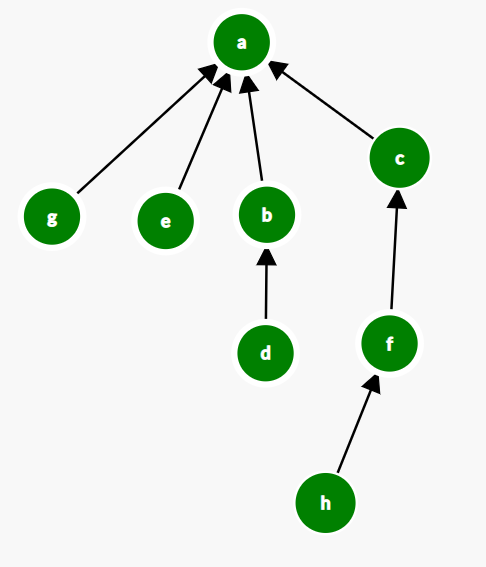
Hence Any further call to find(g)/find(e)/find(c) will be just a single operation task.

The final optimised implementation of combine() & find() are below:

int find(int u)
{
    if(u == representative[u])
        return u;

    else
        return representative[u] = find(representative[u]);
}

void combine (int u, int v)
{
    u = find(u);
    v = find(v);

    if(u == v)
        return;

    else
    {
        if(size[u] > size[v])
        {
            representative[v] = u;
            size[u] += size[v];
        }

        else
        {
            representative[u] = v;
            size[v] += size[u];
        }

    }
}

Note: Huge credit to Sumukh Bhardwaj's post(Invulnerable on Leetcode).