2215 Find the Difference of Two Arrays

Techniques Used

• Hashing

Approach

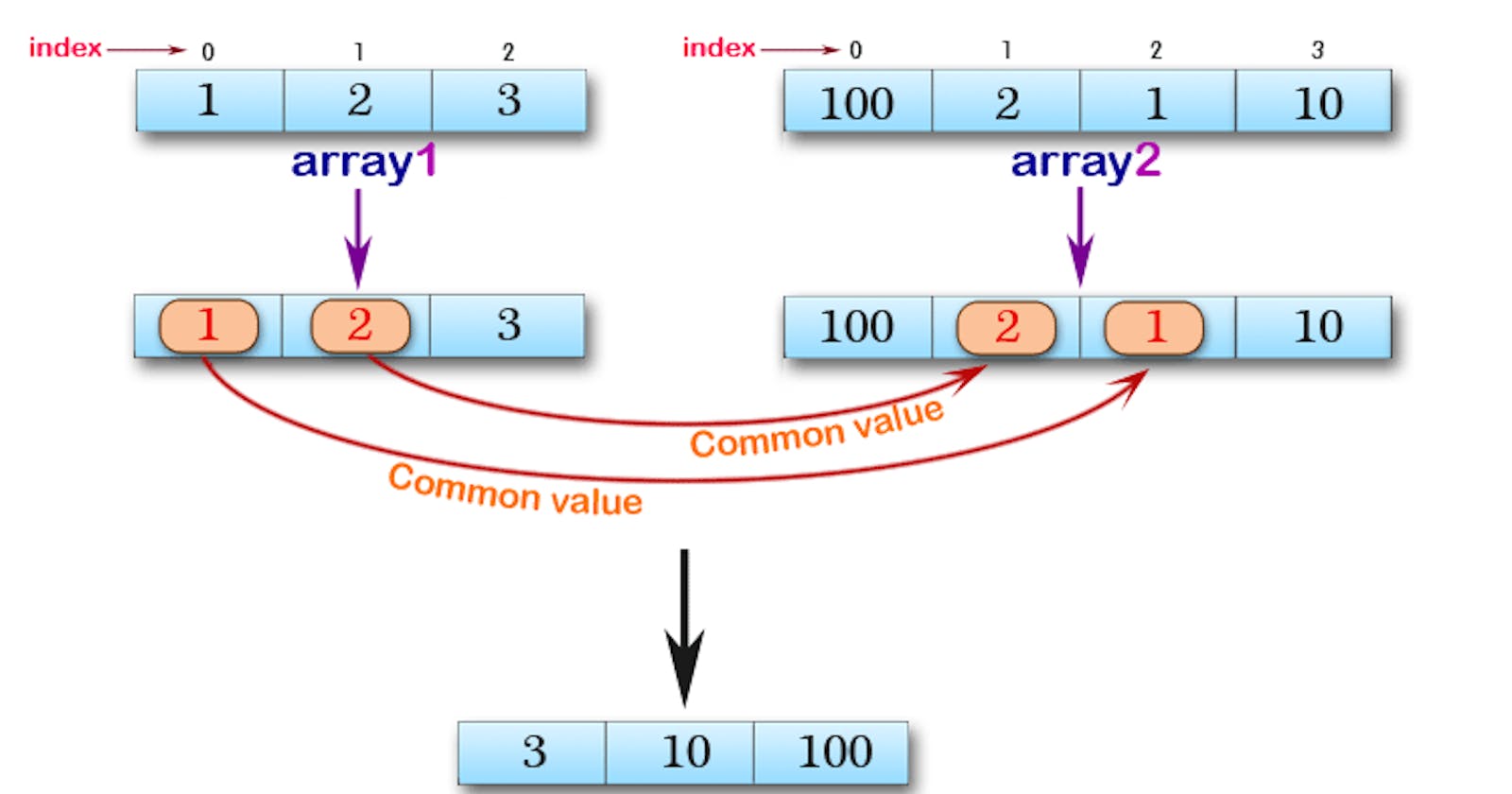
• Initialize two hashsets, and add respective elements from both the arrays to their own sets.
• We did the above so that we can easily find the existence of a certain number in each of the sets easily.
• Loop over the nums1 array elements, if the ith element is contained in s2, then add it to the linkedlist l1.
• Loop over the nums2 array elements, if the ith element is contained in s1, then add it to the linkedlist l2.
• Add both the linkedlists l1, and l2 to the resultant list of lists.

Complexity:

• TIme Complexity: O(N + M)
• Space Complexity: O(N + M)

Code: C++

class Solution {
public:
    vector<vector<int>> findDifference(vector<int>& nums1, vector<int>& nums2) {

        unordered_set<int> s1;
        unordered_set<int> s2;

        for(int i = 0; i < nums1.size(); i++){
            s1.insert(nums1[i]);
        }

        for(int i = 0; i < nums2.size(); i++){
            s2.insert(nums2[i]);
        }


        vector<int> temp;

        for(int i: s1){
            if(s2.find(i) == s2.end()){
                temp.push_back(i);
            }
        }
        vector<vector<int>> res;
        res.push_back(temp);

        temp.clear();

        for(int i: s2){
            if(s1.find(i) == s1.end()){
                temp.push_back(i);
            }
        }

        res.push_back(temp);

        return res;

    }
};

Code: Java

class Solution {
    public List<List<Integer>> findDifference(int[] nums1, int[] nums2) {

        Set<Integer> s1 = new HashSet<>();
        Set<Integer> s2 = new HashSet<>();

        fillHashSet(nums1, s1);
        fillHashSet(nums2, s2);

        List<Integer> l1 = new ArrayList<>();
        List<Integer> l2 = new ArrayList<>();


        for(int i : nums1){
            if(!s2.contains(i)){
                if(!l1.contains(i)) l1.add(i);
            }
        }

        for(int i : nums2){
            if(!s1.contains(i)){
                if(!l2.contains(i)) l2.add(i);
            }
        }
        List<List<Integer>> res = new ArrayList<>();

        res.add(l1);
        res.add(l2);

        return res;


    }

    static void fillHashSet(int[] nums, Set<Integer> set){
        for(int i : nums){
            set.add(i);
        }
    }
}